Hilbert space theory

Author: fbcl

August undefined, 2024

WebNov 27, 2024 · Sorted by: 4. It is actually surprisingly complicated to give an answer to this that is even halfway satisfactory; Hilbert spaces are very unusual. First, your question about metric spaces is easier to answer: you can take the morphisms to be short maps, which are maps f: X → Y satisfying. d Y ( f ( x 1), f ( x 2)) ≤ d X ( x 1, x 2). This ... WebThe book presents an introduction to the geometry of Hilbert spaces and operator theory, targeting graduate and senior undergraduate students of mathematics. Major topics discussed in the book are inner product spaces, linear operators, spectral theory and special classes of operators, and Banach spaces.

Spectral Theory in Rigged Hilbert Space - Department …

WebLecture 14: Basic Hilbert Space Theory (PDF) Lecture 14: Basic Hilbert Space Theory (TEX) The norm induced by the inner product on a pre-Hilbert space; Hilbert spaces; Orthonormal and maximal orthonormal subsets of a pre-Hilbert space; Week 9. Readings: [RM] Chapter 3, Sections 5–6 and Chapter 4, Section 1. WebThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the... green lighted christmas tree

[1611.09029] Quantum theory in real Hilbert space: How the …

WebHilbert space is a vector space H over C that is equipped with a complete inner product. Let’s take a moment to understand what this means; much of it will be familiar from IB … WebAbstract. We present a short introduction to Hilbert spaces and linear operators deﬁned on them. 1. Introduction Hilbert spaces are the closest generalization to inﬁnite dimensional spaces of the Euclidean spaces. These notes were written for students wishing a basic introduction to Hilbert space theory but who have no knowledge of Banach ... WebHilbert Spaces Recall that any inner product space V has an associated norm de ned by kvk= p hv;vi: Thus an inner product space can be viewed as a special kind of normed … green meadow dr columbia md

hilbert space - What is a fermionic field theory? - Physics Stack Exchange

An Introduction to Reproducing Kernel Hilbert Spaces and …

WebA general theory of measurement context effects, called Hilbert space multidimensional (HSM) theory, is presented. A measurement context refers to a subset of psychological … WebNov 28, 2016 · Quantum theory in real Hilbert space: How the complex Hilbert space structure emerges from Poincaré symmetry Valter Moretti, Marco Oppio (Trento U.) As … green marble wash basinWebC of complex numbers. A Hilbert space a special kind of vector space. This article starts with the general idea of a vector space over C and then walks through a series of specializations to arrive at the idea of a Hilbert space.1 Quantum theory uses only separable Hilbert spaces, which satisfy an extra condition that is closely green machine juice nutritional information

"Webfocus will be on Hilbert space theory and applications as well as the theory of linear operators on Hilbert space. We show how Hermitian operators are used to represent … " - Hilbert space theory

Hilbert space theory

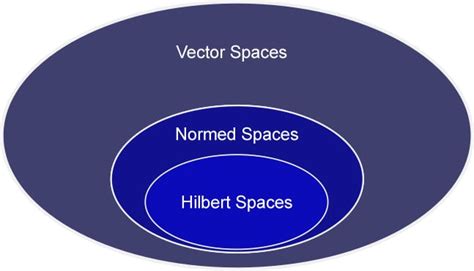
Hilbert space and group theory: relationship between …

WebHilbert space, in mathematics, an example of an infinite-dimensional space that had a major impact in analysis and topology. The German mathematician David Hilbert first described this space in his work on … Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. See more In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. … See more Lebesgue spaces Lebesgue spaces are function spaces associated to measure spaces (X, M, μ), where X is a set, M is a σ-algebra of subsets of X, and μ is a countably additive measure on M. Let L (X, μ) be the space of those complex … See more Pythagorean identity Two vectors u and v in a Hilbert space H are orthogonal when ⟨u, v⟩ = 0. The notation for this is u ⊥ v. More generally, when S is a subset in H, the notation u ⊥ S means that u is orthogonal to every element from S. See more Motivating example: Euclidean vector space One of the most familiar examples of a Hilbert space is the See more Prior to the development of Hilbert spaces, other generalizations of Euclidean spaces were known to mathematicians and physicists. … See more Many of the applications of Hilbert spaces exploit the fact that Hilbert spaces support generalizations of simple geometric concepts like See more Bounded operators The continuous linear operators A : H1 → H2 from a Hilbert space H1 to a second Hilbert space H2 are bounded in the sense that they map See more

Did you know?

WebAn RKHS is a Hilbert space (Akhiezer and Glazman:1963) in which all the point evaluations are bounded linear functionals. (Unlike L2.) Letting H be a Hilbert space of functions on some domain T , this means, that for every t 2 T there exists an element t 2 H , such that f(t)=< t;f >; 8f 2 H; where <;>is the inner product in H. Let < s; t >= WebApr 16, 2024 · The Hilbert space H is part of the data that defines a QFT model. This Hilbert space does not need to be a Fock space. To answer your second question, the Wightman …

WebOct 26, 2024 · This book contains the best introduction of quantum mechanics in chapter 1 and chapter 2, using rigorous group representation theory in Hilbert space, but is very … Webits applications, the analysis, through spectral theory, of linear operators T : H 1!H 2 between Hilbert spaces. The emphasis of the course is on developing a clear and intuitive picture, …

WebSpectral Theory in Rigged Hilbert Space where fφkg ˆ n, f kg ˆ m, and fFkg ˆ n are orthonormal bases and the k are positive numbers such that ∑1 k=1 k <1: (14) In this … WebIntroduction To Hilbert Spaces Pdf Recognizing the exaggeration ways to get this books Introduction To Hilbert Spaces Pdf is additionally useful. You have remained in right site to begin getting this info. acquire the Introduction To Hilbert Spaces Pdf belong to that we meet the expense of here and check out the link.

WebFeb 16, 2024 · Hilbert space means the complete space endowed with inner product. The elements of the Hilbert space could be any vector including real, complex and function. Completeness is defined with very complicated concepts but we can consider the completeness that there is no hole at the space. The more important concepts for data …

WebGilbert Helmberg, Introduction to Spectral Theory in Hilbert Space (North-Holland, Amsterdam 1969; corr. 2nd pr. 1975; repr. Dover 2008 (?)) N. Young, An Introduction to Hilbert Space (Cambridge University Press 1988) Share Cite Follow answered Aug 19, 2016 at 17:10 community wiki Calum Gilhooley Thanks. green machine 62v cordless mowerWeb978-1-107-10409-9 - An Introduction to the Theory of Reproducing Kernel Hilbert Spaces Vern I . Paulsen and Mrinal Raghupathi Frontmatter More information. ... 2.1 Hilbert space structure 17 2.2 Characterization of reproducing kernels 23 … green johanna compost bin irelandWebDec 12, 2014 · In this chapter, we will consider the spectral theory for compact hermitian operators on a Hilbert space. 7.1 Basics of Hilbert Spaces Before we begin our discussion … green mill closingWebMar 25, 2024 · David Hilbert, (born January 23, 1862, Königsberg, Prussia [now Kaliningrad, Russia]—died February 14, 1943, Göttingen, Germany), German mathematician who reduced geometry to a series of axioms and contributed substantially to the establishment of the formalistic foundations of mathematics. His work in 1909 on integral equations led to … green mountain alltrailsWebIntroduction To Hilbert Spaces Pdf Recognizing the exaggeration ways to get this books Introduction To Hilbert Spaces Pdf is additionally useful. You have remained in right site … green motion riga green motion solutionsWebOften the term “Hilbert space” is deﬁned to be an inﬁnite-dimensional space, but in this course we will refer to any of the vector spaces of wave functions that occur in quantum mechanics as Hilbert spaces, even when ﬁnite-dimensional. green mountain biltmore flooring